Tiling Separable Convolution in CUDA

※ The code of this post is available in here.

    When we are doing image processing on a GPU, one of the key idea is 'Tiling'. Tiling cuts the image into small rectangles, and tackle those rectangles one by one. It helps to localize the data and improve the cache hit rate. This article discuss how to use it to improve the performance of separable convolution in CUDA.
 

Concept of Tiling

    For CPU, tiling is also called loop-nest optimization. In some problems -e,g the image rotation, tiling is able to limit the memory accessing bound in a region, it avoids the cache being flushed frequently. For GPU, it is much natural : because GPU is matrix machine essentially : A NVIDIA's  streaming multiprocessors (SMP) contains dozen to hundred of cores, and a GPU has several to dozen of SMPs. Therefore, tiling the data is actually to allocate the work to each SMP.

Tiling on GPU

    In most GPU cases, tiling strategy affects the performance mightily. As CPU, a good tiling could increase the cache hit rate. Cache missing, means the data need to be loaded from memory instead of from cache, and the memory accessing, called memory latency, is much slower the arithmetic operations, bring the low performance;  The tile size not only affects cache hit rate,  also influences the SMP usage rate (NVIDIA uses the term "achieved occupancy"). Only in the very simple cases, for example, the vector arithmetic, are little affected by the selection of tile size.

     In NVIDIA Pascal architecture, a SMP is able to run 2048 active threads at one time. Those threads will be allocated to each warp, which comprises 32 lines. CUDA launches SMP in unit of warp,  if the thread number in x-dimension is not an integer multiple of 32, it still need an entire warp to run the remainder - even there is only one thread. Based on this reason, the block size should be as a multiple of 32 as possible. 

     The tiling strategy depends the procedure. If the procedure is pure row-accessing (horizontal), it may be an excellent choice for the block size being (1024, 1); But if the procedure involves column-accessing (vertical), the horizontal 1D block size may not be a good choice, since the block shape would make some lines in the warps idle. We will see how block shape affects the performance.

Separable Convolution

    Separable convolution is a very important concept in image processing or machine learning. If the kernel matrix is product of the 2 vectors, the convolution could be reduced as two of 1D convolution, which reduce an O(N^2) operation to 2*O(N).  More detail about separable convolution please refer to here.

Separable Convolution on CUDA

    Below is the separable convolution CUDA code of row. ( The column code is pretty similar with this one, I leave it out) The outer 2 loops, for height and width, are mapped to the y-dimensional and x-dimensional threads, respectively - i.e. we launch a 2D kernel. Since the length of kernel data is small and the accessing pattern is identical across a warp, we place the kernel data in the constant memory.      The constant memory supports broadcasting, the loaded kernel weightwould be broadcasted to all threads in a single step.  Next, I use the LDG macro (it is the wrapper of __ldg intrinsic) to force loading the input data into the read-only (L2) cache. the code is :

__constant__ float kernel_const_mem[1024];
:
j = blockDim.y*blockIdx.y + threadIdx.y;
for (; j < height; j += blockDim.y * gridDim.y) {

 i = blockDim.x*blockIdx.x + threadIdx.x;
 for (; i < width; i += blockDim.x * gridDim.x) {

  int x, y_mul_input_width;
  int ii;
  float sum;

  sum = 0;
  y_mul_input_width = j*extended_width;
  x = i;

  for (ii = 0; ii < kernel_length; ii++) {
   sum +=LDG(kernel_const_mem[ii])
    * LDG(p_column_done_extended_input_dev[y_mul_input_width + x]);

   x += 1;
  }/*for kernel_length*/

  p_output_dev[j*width + i] = sum;
 }/*for width*/

}/*for j*/

SeparateConvolutionRowGPU << <num_blocks, num_threads >> >
 (width, height, p_column_done_extended_input_dev,
  kernel_length, NULL, p_output_dev);

     The more block we requested, the more warps would be mapped into the SMPs.  If the block number is over the necessity, the SMP recourse would be wasted. Based on this perspective, the choice of the number of blocks (gridDim) is intuitive :  to fill the data as much as possible, and do not waste any block:

gridDim.x = ((width + (blockDim.x -1))/blockDim.x;
gridDim.y = ((height + (blockDim.y -1))/blockDim.y;

     Hence, the question is, how to selection an appropriate block size.

The Selection of Tile Size

    There is a wise phrase in Confucianism :【論語‧子罕第九 】 子曰：「吾有知乎哉？無知也。有鄙夫問於我，空空如也，我叩其兩端而竭焉。」This is to suggest people analyzing the issues from the two extreme cases.  In the matter of the block size, the extreme cases are (1024, 1) and (1, 1024). The runtime result is (including the data transmission time to/from GPU):

input = 1500x1500 kernel = 21x21 100 Rounds	no_ldg	ldg
1024 x 1	268 ms	265 ms
1 x 1024	730 ms	733 ms

 

    This shows CUDA threads is x-dimensional-major  - this is, the L2 cache is designed for the consecutive accessing of thread.x. The (1, 1024) case violates this accessing pattern and the warp size, leads its low performance. Following the Confucius' guide, analyzing the extreme cases is able to clarify the facts: nvprof  proves why the (1, 1024), no_ldg case is the worst : the cache hit rate is zero, and its low occupancy.

 

no_ldg Column/Row	Unified Cache Hit Rate(%) C/R	Achieved Occupancy C/R
1024 x 1	50.1/48.3	0.706/0.68
1 x 1024	0/0	0.588/0.606

     Denote that the occupancy are not high in the both 2 cases, it implies there is still room to improve the performance. It is make sense : there is 2 procedures in the separate convolution, column and row . The block (1024, 1) does not fitting the procedure pattern of column i.e. some lanes in the warps would be idle, so it must not be the best. Below is the result for all block sizes of power 2.

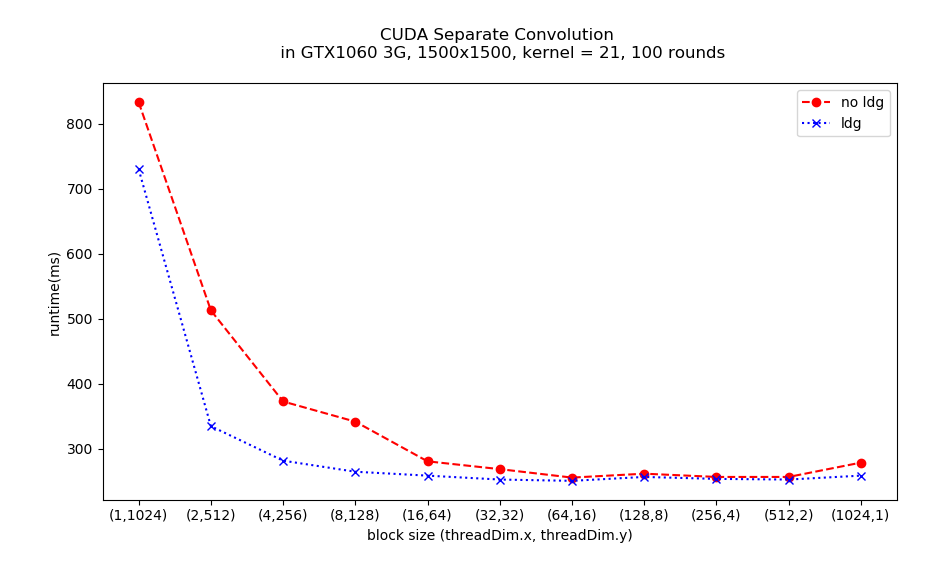
     The performance of (64, 16), (128, 8), (256, 4) and (512, 2) are almost the same. The best one is (64, 16) both for no_ldg and ldg.  nvprof shows the performance is highly related to the cache hit rate and achieved occupancy:

no_ldg Column/Row	Unified Cache Hit Rate(%), C/R	Achieved Occupancy, C/R
16 x 64	38.3/38.7	0.818/0.777
64 x 16	50.1/48.3	0.829/0.793
512 x 2	50.1/48.3	0.831/0.784

     Using __ldg intrinsics would force keeping the data in L2 cache, again, nvprof confirms  __ldg makes the cache hit rate high. Beware that if the block size is too "tubby" (e.g. 1024 x 1 ) or too "slender" (e.g. 2 x 512), the cache hit rate and occupancy are still low, in spite of  __ldg has been adopted.

ldg Column/Row	Unified Cache Hit Rate(%), C/R	Achieved Occupancy, C/R
2 x 512	68.8/60.1	0.753/0.72
16 x 64	88.5/92.2	0.744/0.828
64 x 16	88.8/94.8	0.742/0.812
1024 x 1	56.6/95.1	0.66/0.695

      If block size is tubby, it brings the L2 cache needs to be flushed frequently in the column procedure; whereas the slender case, the performance deserves being low for its shape violating the rule of consecutive accessing and the warp width. Therefore, the block size affects the performance immensely.     

     A good selection is able to achieve good cache hit rate and high occupancy. Especially the cache hit rate, it dominates the speed. However, the best runtime amount these cases is still little worse than the full optimized code using shared-memory which I covered in another blog. But selecting a good block size plus using '__ldg' intrinsic is much easier than rewriting to use shared-memory, it is worthwhile.

Summary

一. Select the block size prudently, it heavily affects the performance. The two metrics in nvprof, unified cache hit rate and achieved occupancy, are able to help you to evaluate whether the selected size is appropriate or not. 

二. Using __ldg intrinsics is the icing on the cake, it brings the good selection of block size more performance.